“我数学就是很烂,救不了。”害怕数学的你,不妨试试“大脑喜欢这样学”这本书里的学习方式。
该书作者Barbara Oakley现在是美国奥克兰大学的工业系统工程学教授,但她从小到大数学都不好,数理科目总是不及格,讨厌数学。进入职场后,她发现如果数理不好,很难去培养相关的技能来解决问题,自己会大大受限。所以她决定重新训练自己的头脑,并逐渐掌握了学习数学的方法,所以写了这本书来分享数学的学习方法。
书中提到,人的大脑在神经学专家的研究下,发现有两种思考方式:“专注式思考”和“发散式思考”。“专注式思考”就是大脑用理性分析的方式来尝试解决问题,你在解数学难题时便是用这种模式;“发散式思考”在你不是专注思考模式时,没有刻意在想某件事,在放空、发呆时,大脑便是处于发散式思考模式。
不知道你有没有一种经验,有时在做很难的数学题,或是思考生活中复杂的问题该怎么处理,在当下一直想不到解法,结果就在散步、洗澡、吃饭时脑中突然灵光一闪,想到了刚刚想了很久都想不到的解法或关键点。科学家研究发现,当你在放空、发呆休息时,大脑并没有停止思考,而是处于发散思考模式,并仍然在持续对问题做思考的连结。
升学顾问机构Candice根据书中的知识和自己的教学经验,归纳出下面几点,希望能帮助学子在准备SAT、ACT等标准化考试时,对数学科目做更有效的学习。
1、专注和放松模式交替
也就是说,如果平时练习数学题想了一阵子想不出来,那就先不理这题,甚至直接休息放空也可,让大脑从专注思考模式切换成发散模式,当你一直在专注模式时,很可能会犯了见树不见林的错误,只能看到题目中的一小部分,然后卡在那,无法从更全面整体的角度来尝试解题,当你放松自己做其他事,这题目如何解决仍在你脑中持续留存,虽然你自己并不会注意到,但大脑会尝试对不同的记忆区块做连结,之后如果突然想到怎么解了,这便是真的学懂了这题型,而且会记得特别牢,不容易忘掉。
2、多利用回想来学习
有学生练习数学题的方式是用看的,他把数学题目的解题步骤用看的,只要自己有看懂步骤,便认为自己会了,这其实是很不推荐的学习方式,建议练习数学题时,应该是做完一部分题目后,要复习时不要去看,尝试在脑中回想刚刚的题目和解法,看自己是否能清楚地回想,然后再动手计算过一次,都没问题,才能说真的会了。
3、不要过度刷题
不要重复一直刷考古题,有的学生喜欢刷题,因为那有一种掌控感,反复做自己已经会的题目,让自己很有成就感。但只能说,这样对真正实力的进步收效甚微,应该是做完一份考古题后,将自己错哪题,为什么错,该如何正确解,记录下来,反复检讨,虽然很辛苦。
4、切割目标
人很难对较远的大目标做出好的规划,所以将大目标切成小目标,安排进自己的行程表中,这才会是有办法好好完成进度表的技巧。
5、考试前一天让自己放松
还记得专注式思考和发散式思考吗?到考前一天,不要再很认真专注的做题目,稍微让自己放松一下,看看自己的笔记,做一些经典题维持手感即可,其馀时间做一些自己喜欢的休闲活动,让自己的大脑处于发散模式,统整过去几个月的记忆区块,好好为了第二天的正式上场做准备。
6、考试时先把题目全部浏览一次
考试的题目有难也有简单的,你先全部看过一遍题型稍微想一下待会大概怎么解,比较难的题目会先留存在你脑中,虽然你写得是别的较简单的题目,但等你回来做难题时,有可能大脑已经把这题所需的记忆区块连结起来了。
从小对数学感到害怕或是想突破数学分数的你,可以从现在开始尝试练习这几个技巧,其实这不是只能用在数学上;专注式思考和发散式思考切换,也十分适合用在创造性的问题。
讲座时间:本周日 8/20 美西时间下午五点/美东时间晚上八点
注册链接:https://www.kyros.ai/counseling-detail/10770?ref=laa7enz
讲座语言:英文
准备好跟Kyros一起踏上丰富多彩的升学之旅了吗!想了解我们的学生如何在行业专家的带领下,逐步迸发创意,并培养产品设计,项目管理及创作能力?
由学生参与设计并为学生服务的Kyros Co-creator 项目(会员可免费申请参与)介绍:
🔍 听听学生们真诚的体验分享和成果展示
🌎Kyros作为业界领先的教育科技平台如何为学生们赋能,在强大的AI技术支持下打造活跃的升学平台,让孩子们“近朱者赤”
🌱探寻 Kyros学生大学申请成绩硕果累累的奥秘,参与我们的优秀学生与学生成长导师的在线讨论!
还在观望吗?Kyros平台有效引导孩子们培养一流大学所看重的领导力,团队合作,求知欲等重要素质。为大学生涯及以后的成功写下浓墨重彩的一笔,快来注册学习吧!

北美家长的数学焦虑:“发现式数学”正在毁掉孩子的未来
一个风和日丽的春日下午,在我女儿就读的加拿大的一所著名私校,布置优雅的小会议室里,正在举行数学课程的家长说明会,起因是家长强烈抗议数学课所谓的创新的计算方法。
空气中有一股剑拔弩张的味道,平时开会多是妈妈们参加,今天则绝大部分是西装革履的爸爸们,还有脸色凝重的副校长坐在最后面压阵。
教学主管略显紧张地开了个头:“我知道,你们的孩子对数学没有信心,家长们也很担忧……”
“对不起!”一位爸爸举起手说:“请你不要说孩子们对数学没有信心,这会严重影响我孩子的自信,他从来没有表现出对数学没有信心,我也从来没有这样说过他。我现在担心的是,学校的数学教育会不会让他没有信心。”
教学主管有点尴尬,赶紧打开PPT开始讲解,他列出了这样一个题:关于248中减去29的方法。
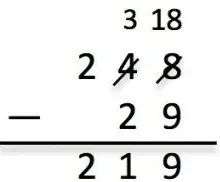
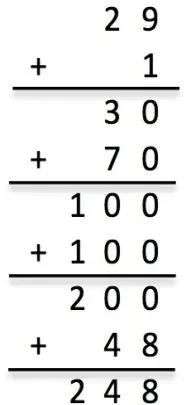
上面上图是使用传统用竖式借位减法。下图是“发现式数学”提倡的创新思维解法,采用容易计算的数字一直计算到248,然后将这些数字加起来得出最终答案。
还没等教学主管讲完,会议室里已经炸开了锅。
一位爸爸大声地说:“为什么不能按照传统的算术标准来计算?一个步骤就可以解决的简单减法要搞得那么复杂吗?这种莫名其妙的计算方法,我们谁都不会,更别说小孩子了。”
“是啊,是啊。”座中另外一位爸爸也接着说道:“上个周末我家开派对,一半的客人都是毕业于常春藤大学的电脑工程师,但是,没有人会做我那三年级女儿的数学作业,这事儿实在是太荒唐了!”
教学主管说:“你们先别着急,我今天的讲座就是要教会你们,然后你们就可以辅导孩子了。”
另一位爸爸站起来生气地说:“我们为什么要学你这种可笑的解题方法?我不会你的解题方法,也没耽误我在多伦多大学,做那么多年的数学教授啊!”……
整整三个小时的说明会,愤怒的家长们没有给教学主管讲下去的机会,家长们的质疑和指责让教学主管狼狈不堪,副校长几次起来阻止都无济于事。最后,闻讯赶来的校长结束了这场“数学战争”。
这是几十年来,北美家长和学校以及教育部门之间,频繁爆发的“数学战争”的一个缩影。
和中国的”传统数学”教育方式不同,受杜威的进步教育主义理论影响,北美采用“发现式数学”(discovering math),主张培养学生的探索知识、解决问题的能力,强调的是思维开发和创新。
但是,北美父母则认为应该向中国等亚洲国家学习,回归“传统数学”教育。在上个世纪九十年代,美国各地爆发过很多家长的抗议活动。家长们联名请愿,或竞选学区委员会席位,甚至还成立许多组织来抵制“发现式数学”。
自2013年起,加拿大安大略省、艾伯塔省和不列颠哥伦比亚省的家长们不断向各省教育厅请愿,指出‘发现式数学’的危害,要求政府修改课程设置,将更多的重点放在基本数学技能上,而不是在发现或创新策略上。
对国内的父母来说,大家担心的是:“传统数学”教育的刷题和死记硬背,往往导致学生缺少创造力和创新能力。而美国数学教学的形式多样,寓教于乐,生动有趣,也在吸引众多的数学教育工作者和家长们。
为什么北美的父母对注重思维创新的“发现式数学”如此反感呢?不仅如此,在北美的历次“数学战争”中,数学家们也是和家长站在一起,呼吁改革数学教育,极力主张采用“传统数学”。难道注重培养数学思维不对吗?
要了解这一切,首先得从什么是“发现式数学”开始。
“发现式数学”如何开发数学思维?
杜威(John Dewey)进步教育,主张遵循儿童的天然意愿、通过儿童自我探索(self-inquiry)的方式来学习。
所以,“发现式数学”的教学方式是以学生为中心,通过思维开发和解决问题(problem solving)能力训练,达到培养学生的创新思维的目标。
跟“传统数学”以老师讲解为主不同,“发现式数学”的老师在课堂上讲得少,以学生自己思考和探索为主。
“小组讨论”(group learning)和“团队合作”(teamwork)是常用的学习方式,3-5个学生围成一桌,由老师提出问题,孩子们通过查阅资料,相互讨论和合作找到解决方案,最后由老师总结。这种方式既培养了独立思考、解决问题的能力,又培养了合作精神。
还有项目式学习(Project-based Learning),女儿做过一个装修房子的数学题,由五个小朋友共同完成。3000元的预算,老师给出了房间的宽度和长度,并要求买一张床、一个书桌和椅子等若干家具。
虽然只涉及到简单的加减乘除,但是,很考验解决问题的能力。从日常生活中认知数学概念和原理,有利于学生对知识的理解深度和运用能力。
“传统数学”要求学生通过枯燥的练习来熟悉和掌握公式、原理和法则;“发现式数学”不主张背诵乘法表和大量重复练习,认为这种死记硬背的方式不仅不利于理解数学概念,还会伤害孩子的创造性。
女儿学校的数学回家作业是不多的,跟中国的题海战术简直是天壤之别。
“发现式数学”认为,重要的是理解数学概念、公式和法则背后的逻辑关系,而不是简单地记住数学知识。所以,老师尽可能不去教授公式或者标准解题方法,而是鼓励学生自己去推理公式、发现概念和找到解题的办法。
就小学算术来说,“发现式数学”认为小学生们不应使用传统的加、减、乘、除的计算方法,而是采用创新的计算方式,甚至自己发明一些新的方法,这样更有利于开发学生的创新思维。
所以,学生们常常以图示法、估算法来代替标准的计算方法。
例如5+2,小朋友不会直接给出结果是7,而是会画冰淇凌、格子、鲜花、各种小动物…… 这种方式直观又生动,可以帮助孩子理解数字的概念以及加法背后的真正含义,而不像是国内的死做题。
例如3×5,正确做法不是通过乘法口诀直接获得15,而是通过3+3+3+3+3或者5+5+5的方式,目的在于理解乘法运算背后所包含的逻辑关系,数字的构成规则,从而能够灵活运用数字。
对较大数字的乘法,通过分解成小题目完成。例如25×44,可以通过将44分为4组(每组11个)和100组(11个)来找到答案1100。
“发现式数学”主张一题多解,来培养学生思维的广阔性和灵活。例如15 x 12,会要求学生通过以下五种不同方式解决问题:

“发现式数学”通过让学生不断自我发现、自我探索和不断创新,加深对隐藏在数字后面的概念的理解,而不是对算术法则的死记硬背和大量练习。
再看看下面这道题,北美孩子的数学其实一点也不简单。
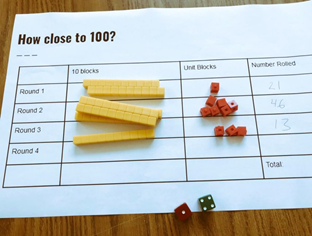
这是要求学习2位数字加法的学生玩“如何接近100?”的游戏,目的是“练习”他们对加法的理解。
在这个游戏中,孩子们被要求通过不同的方式来使用数字,例如10个骰子为一组和单个的骰子,同时还可以尝试不同的组合策略。
和“传统数学”的老师直接教授和学生刻板练习相比,“发现式数学”让数学的学习过程不再无聊,而是充满了思维创新的刺激和挑战,甚至变得很有趣。
虽然教学进度慢,学的内容也少,但是在我看来,花了那么多时间培养孩子的数学思维和逻辑思维,一旦孩子的批判性思维、创造性思维和解决问题能力建立起来了,日后一定会产生厚积薄发的效应。
这就是为什么,美国在高科技领域傲视群雄的原因吧。
“发现式数学”的致命缺陷是什么?
一位女儿同学的家长曾经提醒我,千万不要被五花八门的创新思维开发给迷惑了,加拿大学校的数学课学不到什么东西的,学生的基本知识和基本技能很差,想要学好数学,最好去报个课外班。
我当时没太在意,因为我觉得数学思维才是数学的核心能力。但是,随着女儿年级的提高,加拿大学生数学基础之差,不仅超过了我的想象力,也超过了我的承受范围。
女儿小学一年级才学会如何数到一百,三年级一位数的乘法就可以把她难倒。五年级的时候,10以内个位数的乘法和除法还有问题,我开始担忧了。
六年级的时候,国内小学生已经加减乘除、分数运算滚瓜烂熟了。女儿只学会15以内的加减乘除,在班上已经属于数学很好的孩子了。班上大部分孩子单个数的乘法和除法有问题,看到分数更是胆战心惊。
如果小学生无法构建起基本的乘除法、分数小数、比例和百分比等基础算术技能,恐怕无法适应中学的代数和几何学习,更别提什么创新思维和创造力了。

我不由得倒吸一口冷气,再看看那些统计数据,更让我大惊失色。
加拿大2017年安大略省标准化考试结果显示,只有50%的6年级学生达到省数学标准。
美国的情况也好不到哪儿去,2017年全国教育进步评估:只有33%的初二学生符合年级水平。30%以上的美国理工类大学生必须重新补习中学数学知识,50%学生最终因为数学不行而转专业。
更让人忧心忡忡的是,随着数学在各行各业的重要性日益凸显,北美学生的数学之差已经直接影响到未来职业前景,可以说,数学不好的学生未来人生前景黯淡。
美国劳工统计局指出:2016年到2026年,从事数学有关职业的就业人数将增长28%。
但是,美国的Business Round table调查发现,3/4的CEO认为找不到合格员工。美国80%的中等技术工种(相当于大专)需要更好的数学和计算机技能,大部分职位处于空缺状态。
加拿大的情况也非常类似。

为什么看上去如此完美的“发现式数学”,会是这样一种结果?
按照美国数学家的解释是:“发现式数学”在思维开发和解决问题能力上确实有明显优势,非常适合培养天才学生,这也就是为什么美国可以出现那么多数学牛人和科技大咖的原因。但是却毁掉了普通孩子的数学能力。
因为“发现式数学”有一个致命的缺陷:过于强调教思维训练而忽视数学的内容,导致学生缺乏系统性的数学知识和基本技能,从而也使得创新性的教学方法无法达到应有的效果。
例如就小学阶段来说,“发现式数学”最大的问题是,大大削弱了算术这块内容。
算术中包含着丰富的逻辑推理,有了良好的算术基础,对于培养学生的分析与创造性思维是极其有益的。
对普通学生们来说,只有通过记忆和反复练习来掌握算术基本技能后,才能培养更复杂的逻辑思考能力,否则根本谈不上创新。
而且“发现式数学”提倡用替代性的方式来取代标准计算方法,名义上是创新和探索,这些方法实质上既慢且笨,纯属画蛇添足;常常由于过于复杂和令人费解,让大部分学生莫衷一是,最后哪种方法也掌握不了。
1999年全美220名著名教授发表公开信,要求保持传统数学的标准计算方法,从而引发美国历史上著名的“数学战争”。
但由于“发现式数学”根基深难撼动,在强大的进步教育家面前,数学家们不免势单力薄,最终在“数学战争”中败下阵来。
更糟糕的是,自从2010年美国颁布《州共同核心数学标准》,北美的数学教育不仅没有回归“传统数学”,反而在所谓的创新道路上越来越远,小学的计算方法越来越难懂,即使是从数学相关领域毕业的父母也无法辅导作业。
这也就是为何会发生本文开头我女儿学校家长强烈抗议的故事。家长们由于无法辅导孩子的简单的算术而深陷焦虑,看看推特上美国家长的吐槽:
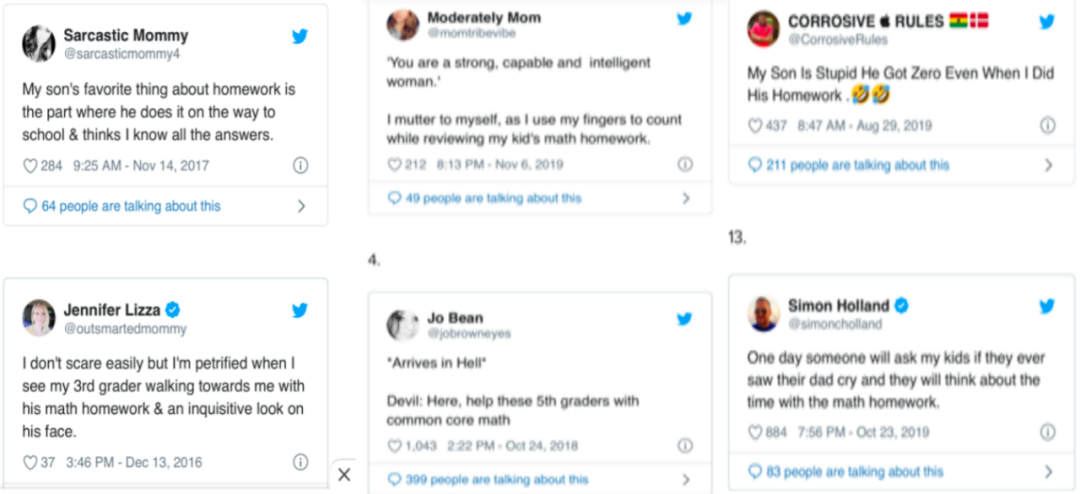
“当我检查孩子数学作业时,我总是这样鼓励和安慰自己:“你是一个坚强,能干和聪明的女人”。
“又要辅导我家五年级孩子的功课了,简直像来到了地狱。”
“我孩子的数学作业是我做的,可是他得了零分。”
“如果有人问我家孩子,是否见过他们的爸爸哭过,我的孩子一定会告诉他们,那是在爸爸辅导数学功课的时候。”
“我儿子喜欢在我送他上学的路上做功课,他以为我可以帮助他。可是我不行啊。”
“我这人啥都不怕,就怕我家那个三年级的孩子让我辅导数学功课。”
未来社会不仅需要大批的尖端数学人才,普通劳动力的数学素质也成为关键因素,数学已经成为每个人立足于社会的核心生存能力。
而“发现式数学”,却连基本的数学知识都未能教给学生,北美家长的抗议会继续,围绕“传统数学”和“发现式数学”的“数学战争”将会旷日持久。
“发现式数学”将何去何从?
女儿六年级下学期的时候,我终于按耐不住内心的焦虑,把她送到一家华人办的数学学校补习。很庆幸这个决定拯救了我女儿的数学,没有让她成为“发现式数学”的牺牲品。
加拿大华人开设的数学学校,采用的是“发现式数学”和“传统数学”相结合的模式。短短几个月,女儿的数学突飞猛进,小学算术运算很快过关,原来学得模模糊糊的那些概念也清晰起来。
和女儿学校不主张大量的课后练习不同,数学学校认为应当刷题,但刷题的目的是为了锻炼思考能力,而不是死记硬背。
每星期一次课,作业大概有十道题,除了几道基本题比较容易之外,其他的题目都有一定难度。这些题都是精心设计的,涵盖大量的知识点。
孩子在做的过程中,思考层层递进,像爬山一样,每步之间都是思维运动的自然进步,每做完一道题的过程,就是一个大量思考的过程,相当于做了几十道普通题。

数学学校校长跟我说,“发现式数学”鼓励学生自己探索知识,独立思考和创新,在数学思维开发上确实有很大的优势。
相比之下,“传统数学”倾向于老师的直接灌输,对学生的启发不够,尤其是题海战术确实伤害了学生的创新性思维。
数学学校有一些国内受过教育的孩子,这些孩子数学成绩整体上超过本土的孩子一大截。但是他们的短板也非常明显,遇到新知识和新问题,往往束手无策,而且不会举一反三,总是习惯性地等待老师来教。
原因就在于:他们习惯用刷题来熟悉和掌握知识,这种死记硬背的方法没有培养学生的逻辑思维和抽象思维,所谓的优势并不能持续很久,等到遇到更多更高级更难的数学知识,会因为数学思维跟不上而感到吃力。
按照数学学校校长的说法,最理想的数学教育就是“发现式数学”和“传统数学”相结合的模式。
一个有力的证明就是,加拿大数学学校最拔尖的、能拿数学大奖的基本都是本土长大的孩子,他们通过“传统数学”熟练掌握算术和概念,通过“发现式数学”会锻炼逻辑思维能力,创造性地运用数学知识解决问题。
北美奥数国家队成员基本都是本土长大的华裔,就是这个原因。

事实上,北美数学好的孩子除了参加课外补习学校外,还可以去考一些公立教育系统的精英教育项目,例如加拿大的天才班、IB、Tops和MacS等,而这些特殊教育项目,也都是采取了“传统数学”和“发现式数学”融合的模式。
北美的数学家们也在讨论“传统数学”和“发现式数学”如何相融合,他们讨论了两种模式分别应当什么阶段实施?或者两者在学校的教育中,各自应当占多大的比例。
目前一个比较普遍的观点是:
小学阶段还是以“传统数学”为主,学生应该通过记忆和练习来获得基本的知识和技能;
从小学高年级开始更注重思维开发,逐渐转向“发现式数学”。
约翰霍普金斯大学数学系教授W. Stephen Wilson这样说:“人们以为能够在小学的数学课堂里教会学生创造性。忘掉创造性吧,只要能对直白的问题给出直截了当的解答就可以了。”
温尼伯大学教授Anna Stokke认为,小学应当优先考虑“传统数学”,有了扎实的基础知识后,当中学数学变得更加抽象时,学生们就不会再迷失。
Anna教授在2015 年提出了具体建议:
将80%的教学时间用于“传统数学”,如背诵九九乘法表和做传统的加减乘除;
20%的教学时间用来进行“发现式数学”,例如使用图示法和创新的解题方法。

目前,加拿大小学数学已出现向“传统数学“回归的现象。
阿尔伯塔省的小学生开始背九九乘法表;
曼尼托巴省开始向学生教授加减乘除的标准计算方法;
安大略省从去年开始重新推出传统的数学教学方法,如背诵九九乘法表和加减乘除法等。
可以预见,两种模式的融合应当是未来北美数学教育的方向。
对渴望在数学思维开发上有所突破和创新的中国来说,应当坚持传统的“基本知识和基本技能”优势基础上,引进和借鉴“发现式数学”的教学方式。
千万不要抛弃基础教育阶段的现有优势,全盘追随“发现式数学”,以免重蹈北美数学教育失败的覆辙。
参考资料:
2. 《伍鸿熙:看着一群人正在败坏数学,使我很愤怒——谈美国中小学数学教育》



